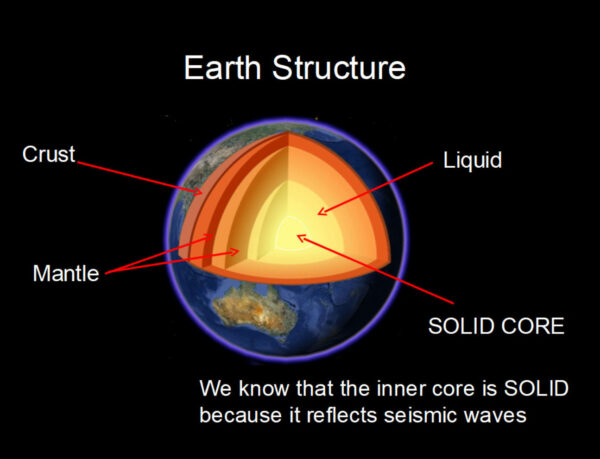
There exists a widespread belief that a discrete series of samples does not contain enough information to reconstruct the continuous process that these samples represent. This article demonstrates that for a given series of discrete points there exists only one continuous process that has the bandwidth precisely equal to the Nyquist frequency.
Estimating Accuracy of GPS Doppler Speed Measurement using Speed Dilution of Precision (SDOP) parameter
This article presents a method for estimating the accuracy of GPS-Doppler speed measurement using Speed Dilution of Precision (SDOP) parameters newly introduced by SiRF. Direct measurements of GPS-Doppler speed errors are confronted with theoretical SDOP predictions. Comparison reveals that SDOP is a very useful and practical parameter for determining accuracy of GPS-Doppler speed measurement. It […]